1. Modelul  Behrens-Feichtinger

 

                O serie întreagă de modele „fizice” microeconomice au fost elaborate, dintre acestea unele relativ simple. Ca extensia la economie a modelului neliniar Richardson a cursei înarmărilor [16], pentru care controlul prin aplicarea forţei stabilizatoare poate fi realizat în condiţii optime [10], modelul Behrens-Feichtinger, se referă la două firme având strategii asimetrice de investiţie.

Modelul se referă la evoluţia vânzărilor (xn şi yn) a două firme competitive pe aceeaşi piaţă de bunuri (cu strategii de investiţie asimetrică şi activă pentru ambele firme). Dacă o firmă nu investeşte, în publicitate, cercetare, re-tehnologizare şau dezvoltare este de aşteptat ca vânzările firmei respective să scadă exponenţial, cu un factor ce caracterizează situaţia concretă de pa piaţă a firmei, şi fiecare firmă are posibilitatea să investească pentru a-şi creşte vânzările. Fiecare firmă are o abordare diferită a strategiei de investiţie, firma X investeşte numai dacă are un avantaj asupra firmei Y, iar cealaltă firmă dor dacă are o poziţie dezavantajoasă. Dacă firma X este mai mică şi nu investeşte – se comportă defensiv, iar firmaY, fiind mai mare, dacă este superioară competitorilor, nu investeşte nici ea– se comportă agresiv. Putem deci descrie o evoluţia a vânzărilor celor două firme, într-o scală discretă de timp -  reprezentând valoarea vânzărilor firmei X la momentul n temporal – prin:

,

.

cu a şi b (0 < a, b < 1) fiind ratele temporale la care vânzările ambelor fire scad în absenţa investiţiilor (scădere exponenţială). Ideal funcţia  este o funcţie treaptă definită ca fiind zero pentru  şi egală cu a pentru , dar funcţia treaptă poate fi aproximată cu , unde c caracterizează panta trecerii de la 0 la a pentru funcţie ( reconstituie funcţia treapta), si măsoară gradul de neliniaritate.

               

                2 Dezvoltarea modelului microeconomic

Pentru a adapta modelul microeconomic la condiţii de evoluţie dinamică mai apropiate de condiţiile reale vom introduce o serie de modificări care au ca scop dezvoltarea acestui model matematic şi extinderea aplicabilităţii sale.

.

Natura distribuţiei poate să nu fie Gaussiană, dar acest lucru va fi analizat ulterior. Termenul este echivalent cu introducerea unui zgomot decizional privind momentul la care va avea loc o anumită investiţie.

,

Termenul fiind echivalent cu introducerea unui zgomot în valoarea investiţiilor.

,

unde indicele superior face referire la agentul comercial, pe piaţă fiind M astfel de agenţi. Cuplarea se face prin termenul , presupunând că piaţa este o piaţă cu cerere „fixă” sau lent variabilă, V reprezentând valoare cererii întregii pieţe pentru portofoliul de produse-servicii considerate. Desigur, într-un model mai elaborat, valoarea acestei mărimi va putea depinde de suma investiţiilor agenţilor comerciali (prin generarea şi condiţionarea interesului pentru produse...), de mărimi care să vină din exteriorul sistemului considerat, creşterea sau scăderea puterii de cumpărare, a oportunităţilor sau modificarea legislaţiei, etc.

Analiza dinamicii neliniare a modelului microeconomic

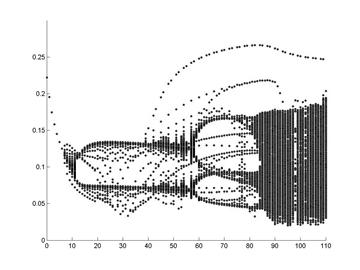
Interesant de arătat că în funcţie de valoarea coeficientului c avem de a face cu diferite evoluţii temporale ale sistemului, în Figura 5 fiind reprezentat arborele cu bifurcaţii realizat pentru cazul , reprezentând domeniul de valori posibile pe care le poate lua variabila X funcţie de modificarea coeficientului c.

 

 

 

 

 

  

 

 

Fig. 5. Arborele cu bifurcaţii realizat pentru variaţia coeficientului funcţiei „treaptă”

 Se observă că o manifestare haotică este condiţionată de valori mari ale coeficientului c, ceea ce înseamnă o pantă mare a funcţiei treaptă!

Expresiile care vor definii dinamica neliniară a modelului microeconomic sunt:

unde a, b şi c sunt parametrii de investiţie (constante pozitive). Termenul neliniar descrie influenţa investiţiei la timpul n asupra vânzărilor la timpul (n+1). În figura de mai jos este prezentată evoluţia temporală a vânzărilor firmei X, pentru setul de coeficienţi de mai sus, pentru

 

 

 

 

 

 

  

Fig. 6. Seria temporală haotică, discretă, a vânzărilor firmei X.

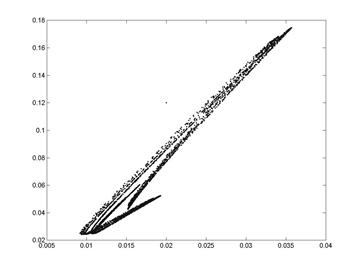
O altă serie de informaţii pot fi obţinute din analiza traiectoriei dinamice a sistemului în spaţiul stărilor (fazelor). În figura de mai jos prezentăm, pentru aceeaşi parametrii şi valori iniţiale evoluţia traiectoriei necontrolate, care este 2D datorită numărului de variabile libere.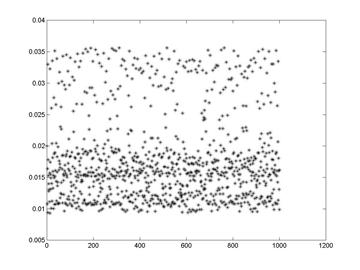

 

 

 

 

 

 

  

Fig. 7. Evoluţia în spaţiul fazelor pentru sistemul necontrolat

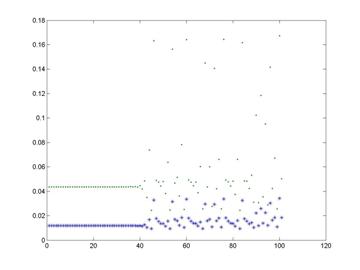
             În analiza dinamicii sistemului o altă caracteristică importantă este acea a poziţiei punctelor fixe, punctele de iniţializare ale stării sistemului pentru care traiectoria în spaţiul fazelor este punctuală, sistemul îşi conservă valorile variabilelor. Un calcul sumar arată o valoare a punctelor fixe , pentru parametrii prezentaţi mai sus. Existenţa  dinamicii haotice este încă odată pusă în evidenţă de evoluţia temporară a variabilelor X şi Y, vezi figura de mai jos, unde datorită limitărilor în precizia

 

 

 

 

 

 

 

Fig. 8. Evoluţia variabilelor X şi Y în apropierea punctelor fixe

calculelor, punctele fixe găsite sunt aproximative, traiectoria temporară redevenind haotică după un număr de paşi temporari datorită abaterii acestora de la valoarea exactă şi dependenţei exponenţiale a traiectoriilor haotice de valorile iniţiale.

Predictibilitatea haosului este limitată în ultimă instanţă de puternica dependenţa a traiectoriilor viitoare de condiţiile iniţiale.

 

 

 

 

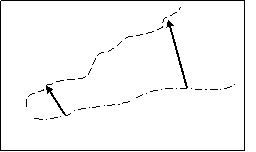
Să ne referim la calculul coeficientului Lyapunov care se referă la modul în care două traiectorii iniţial adiacente, separate de un interval infinitezimal, se separă în timp, , adică

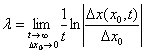 . Dacă se cunoaşte modul de modelare ala datelor cu anumite ecuaţii, putem calcula coeficientul Lyapunov local folosind definiţia sa: . Dacă avem două puncte iniţiale separate prin ,  şi , şi o hartă 1D, , atunci după o iteraţie separarea dintre cele două traiectorii va deveni şi deci . Iar coeficientul Lyapunov global prin mediere pe multe iteraţii . În cazul 2D, , atunci când condiţiile iniţiale sunt separate de  infinitezimal (), şi după o iteraţie traiectoriile sunt separate de  şi , (derivatele parţiale...) şi definim cel mai mare exponent Lyapunov: ,

 adică 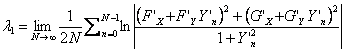, cu  este tangenta direcţiei creşterii maximale (vectorul tangentă), care evoluează conform

 şi este independent de  după multe iteraţii, deoarece oricare două condiţii iniţiale se vor orienta pe direcţia întinderii maxime. Aici  semnifică coeficientul Lyapunov de-a lungul direcţiei maxime de separare a traiectoriilor – primul coeficient Lyapunov.

         În decursul iteraţiilor paralelogramul condiţiilor iniţiale (,) se distorsionează tipic prin alungirea (creşterea separării traiectoriilor) cu preponderenţă a unei direcţii. Aria paralelogramului scade, iar el devine mai comprimat, cu direcţia comprimării schimbându-se la fiecare iteraţie. Această comportare a spaţiului stărilor (micşorarea volumului şi alungirea...) se datorează termenilor din afara diagonalei matricei Jacobian 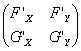,  şi . Pentru a calcula aria paralelogramului după prima iteraţie să observăm că aria paralelogramului, în cazul în care termenii din afara diagonalei matricei Jacobian sunt nuli (nu se deformează, aria dreptunghiului maximal), este , iar regiunea goală are aria , astfel încât aria ce rămâne paralelogramului este , determinantul Jacobian-ului, si deci raportul expandării ariei este . Descriind paralelogramul în termenii direcţiei de maximă separare a traiectoriilor , şi a direcţiei perpendiculare pe aceasta,  în 2D ... şi în 3D, – al doilea coeficient Lyapunov, în acest sistem de coordonate rotit , adică , care generalizează în dimensiuni mai mari suma coeficienţilor Lyapunov (este logaritmul expansiunii raportului hiper-volumului) – a nu se uita că  variază pe orbită şi dă suma coeficienţilor locali Lyapunov. Suma exponenţilor globali se obţine prin medierea  de-a lungul orbitei. Expansiune globală a ariei nu poate să fie pozitivă pentru o orbită mărginită, dacă sistemul are un atractor atunci expansiunea trebuie să fie negativă, corespunzând cu o contracţie a condiţiilor iniţiale pe atractor. Cunoscând determinatul Jacobian-ului şi primul coeficient Lyapunov se poate dermina uşor, pentru cazul 2D, din  al doilea coeficient Lyapunov.

         Pentru a determina dacă un sistem este haotic este suficient să se determine cel mai mare coeficient Lyapunov (), dacă se doreşte estimarea predictabilităţii medii este nevoie de toţi coeficienţii pozitivi, altfel este nevoie de întreg spectrul de exponenţi Lyapunov.

         Pentru calculul numeric a celui mai mate exponent Lyapunov (în orice dimensiune) trebuie să evaluăm numeric derivata de-a lungul direcţiei de maximă expansiune şi să-i mediem logaritmul de-a lungul traiectoriei:  alegem condiţiile şi separarea iniţială în orice direcţie,  şi  (mărimea vectorului ,   trebuie să fie mult mai mică decât scala schimbării curgerii dar de câteva ordine de mărime mai mare decât precizia numerică);  iterăm un pas temporal şi determinăm  şi , prima orbită neperturbată şi a doua cea perturbată;  modificăm poziţia celei de a doua traiectorii de la  la , pentru a menţine orbitele apropiate (la ) pe măsură ce lăsăm direcţia să se orienteze pe cea a maximului expansiunii;  adăugăm mărimea  la o medie dinamică de-a lungul traiectoriei şi sărim la pasul  până când media pare să conveargă. Dacă sistemul este o curgere, se împarte media rezultată  la pasul temporal h astfel încât unităţile să fie cele corecte.

         Dacă avem acces doar la datele directe putem folosii metoda numerică de mai sus cu modificarea că în loc să perturbăm orbita (), căutăm în seria temporală punctele apropiate în spaţiul stărilor ale căror orbite le-am urmărit pentru câţiva paşi temporali sau până ele se separă prea mult, când alegem alte puncte apropiate, dar în aceeaşi direcţie [17]. Algoritmul presupune divergenţa exponenţială dar nu o verifică şi deci nu poate distinge haosul de zgomot. O altă metodă este aceea de a înainta prin seria temporală căutând cel mai apropiat punct  de fiecare punct  din spaţiul împachetat temporal m-dimensional, după care mediem logaritmului ratei de separaţie a acestor două puncte pe următorii k paşi temporali [18]. Cel mai mare coeficient Lyapunov este dat de , la valori intermediare ale lui k (valorile mici ale lui k deoarece punctele nu s-au aliniat pe direcţia expansiunii maxime, iar cele mari deoarece se pot apropia de dimensiunea atractorului şi să cauzeze deviaţii de la exponenţială), aici

         În principiu putem distinge prin această metodă haosul de zgomotul , unde coeficientul Hurst este  (vezi analiza R/S), şi ar trebui să avem , adică panta  nu ar trebui să fie constantă, faţă de cazul haosului unde panta graficului  ar trebui să fie constantă (o regiune substanţială de proporţionalitate  trebuie să fie evidentă în cazul haosului).

         Este foarte importantă cunoaşterea sau estimarea coeficienţilor Lyapunov deoarece de valoarea lor depinde modul de evoluţie a sistemului:

• l < 0: indică comportare convergentă către un atractor stabil sau un singur punct fix

• l > 0: indică comportare haotică, deviaţiile iniţiale cresc exponenţial şi sistemul este  foarte sensibil la condiţiile iniţiale

• l = 0: indică stabilitate marginală. Valorile lui r cu ®l 0: marchează puncte de bifurcaţie unde un atractor devine instabil şi este înlocuit de unul cu perioadă dublă

• l ® - Ą: exponent divergent marchează orbite superstabile în care deviaţiile (apropiate atractorului) dispar extrem de rapid

Coeficient Lyapunov pentru modelul microeconomic, se calculează plecând de la funcţiile de iteraţie ale hărţii

şi este întotdeauna posibil să se scrie o hartă D-dimensională în termenii unei hărţi 1D, proiecţia traiectoriei pe axa de observaţie, folosind termeni întârziaţi ai observabilei, dar în general numărul termenilor întârziaţi depăşesc D).

Matricea Jacobiană (cazul sistemului fără control, de dimensiune 2) este

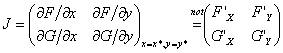
De exemplu, pentru setul de valori iniţiale şi ale coeficienţilor (cu ) , coeficientul  şi ştiind valoarea determinantului , găsim valoarea celui de la doilea coeficient .

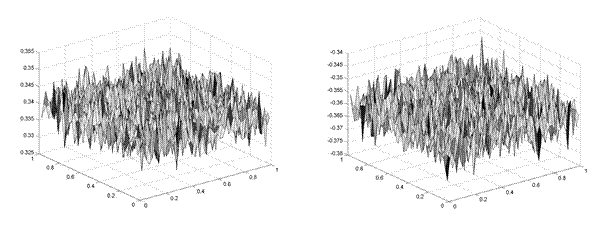
În figurile de mai jos sunt prezentate suprafeţele de evoluţie a valorilor acestor doi coeficienţi, pentru setul de coeficienţi listaţi mai sus, pentru condiţii iniţiale , şi .

 

 

 

 

 

 

 

 

Fig. 9. Suprafeţele de evoluţie a valorilor coeficienţilor Lyapunov 1 şi 2 pentru sistemul „liber”

Se observă că valoarea principalului coeficient Lyapunov este pozitivă, implicând o comportare haotică, indiferent de valorile iniţiale de pornire ale iteraţiilor. Dintr-o analiză similară, funcţie de valorile coeficienţilor, se determină condiţiile pentru apariţia haosului, care sunt .